My Math Academy Learning Workflow

Aug 25, 2024 • 5 min read

Navigating complex Math Academy lessons can be challenging. Over time, I’ve developed a structured approach that has significantly improved my understanding and retention of mathematical concepts. Let me walk you through my process, and hopefully it’ll speed up your learning journey.

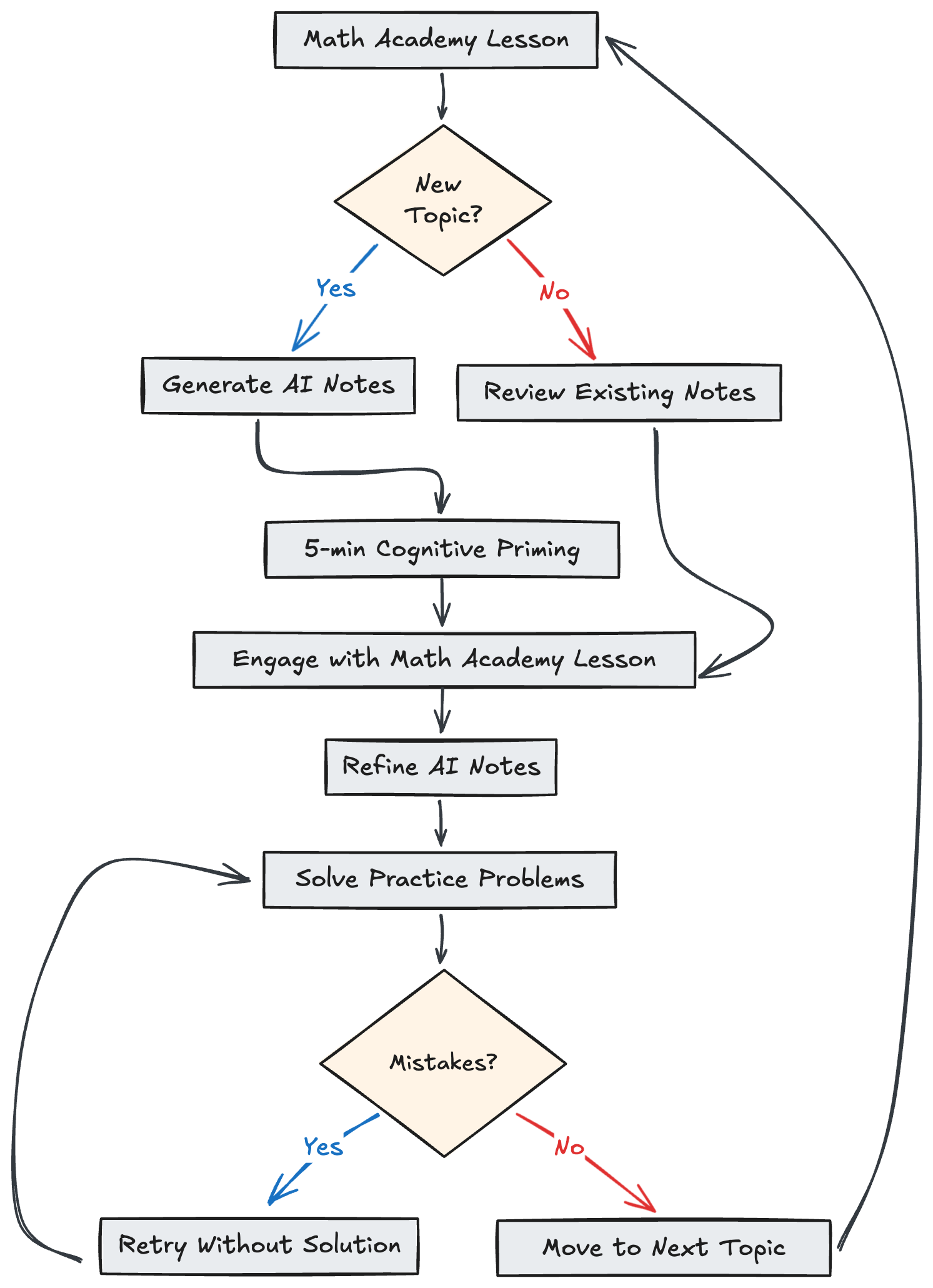
$My Math Workflow$

Here’s how I approach each new Math Academy lesson:

Topic Check: I start by asking, “Is this a new topic?”
- For new topics, I use an AI tool to generate initial notes.
- For familiar topics, I review my existing notes.
Quick Prep: I spend about 5 minutes reviewing the notes. This brief overview helps prime my brain for the lesson.
Math Academy Lesson: With this preparation, I find it easier to follow and engage with the actual lesson.
Note Refinement: After the lesson, I revisit my notes. I add new information, clarify points, and sometimes correct misunderstandings.
Practice Problems: Next, I tackle practice problems. When I make mistakes, I try to figure them out on my own before checking the solutions.
Repeat: I move on to the next topic and start the process again.

AI Prompt Preview:

Create concise mathematical notes (fenced markdown code block) on the topic "[INSERT TOPIC]" using the following structure:

# [Topic Name] ([Area] > [Subarea])
[e.g., "Mean (Mathematics > Statistics)" or "Complex Numbers (Mathematics > Algebra)"]

## Definition
Provide a clear, formal mathematical definition of the topic. Include:
- A concise verbal explanation of the concept
- The mathematical formula or representation, using LaTeX notation
Example: "For a dataset ${x_1, x_2, ..., x_n}$, the arithmetic mean $\bar{x}$ is defined as:
$$\large\bar{x} = \frac{1}{n}\sum_{i=1}^n x_i = \frac{x_1 + x_2 + ... + x_n}{n}$$"

## Key Concepts
- [List 3-4 fundamental ideas or principles related to the topic]

## Important Properties
1. [State a key property or characteristic]
2. [State another key property or characteristic]
3. [State a third key property or characteristic, if applicable]

## Essential Formulas
- [Present a crucial formula, using LaTeX notation]
- [Present another crucial formula, if applicable]

## Core Examples
1. [Provide a basic example demonstrating the concept]
2. [Provide a more advanced application or example]

## Related Theorems/Rules
[If applicable, state any important theorems or rules associated with the topic]

## Common Pitfalls
- [Mention a common mistake or misunderstanding]
- [Mention another common mistake or misunderstanding]

## Related Topics
- [List a closely related mathematical topic]
- [List another closely related mathematical topic]

## Quick Review Questions
1. [Pose a question that tests understanding of a key concept]
2. [Pose another question that encourages deeper thinking about the topic]

Ensure the notes are mathematically accurate, concise, and suitable for quick review. Use LaTeX notation for ALL mathematical expressions, including numbers (e.g., $2$, $\pi$). Use double dollar symbols ($$) for display-style equations or main expressions, and single dollar symbols ($) for inline expressions. The area and subarea in the title should reflect the topic's place in the broader mathematical hierarchy. Use double square brackets [[]] to link to related concepts, theorems, or topics, creating connections between different notes.

Example of AI-Generated Notes:

# Complex Numbers (Mathematics > Algebra)

## Definition
A complex number $z$ is a number of the form $a + bi$, where $a$ and $b$ are real numbers and $i$ is the imaginary unit defined by $i^2 = -1$. Formally:

$$\large z = a + bi, \quad \text{where } a, b \in \mathbb{R} \text{ and } i^2 = -1$$

## Key Concepts
- Real and imaginary parts
- Complex plane representation
- Modulus and argument
- Complex conjugate

## Important Properties
1. Closure: The sum and product of two complex numbers is a complex number
2. Commutativity: $z_1 + z_2 = z_2 + z_1$ and $z_1 \cdot z_2 = z_2 \cdot z_1$
3. Every complex number has a unique complex conjugate

## Essential Formulas
- Modulus: $|z| = \sqrt{a^2 + b^2}$
- Euler's formula: $e^{i\theta} = \cos\theta + i\sin\theta$

## Core Examples
1. Simplify $(3 + 2i) + (1 - 5i)$
2. Find the roots of $z^2 + 1 = 0$

## Related Theorems/Rules
Fundamental Theorem of Algebra: Every non-constant polynomial equation has at least one complex root

## Common Pitfalls
- Forgetting that $i^2 = -1$ when simplifying expressions
- Incorrectly applying properties of real numbers to complex numbers

## Related Topics
- [[Polar Form of Complex Numbers]]
- [[Complex Roots of Unity]]

## Quick Review Questions
1. What is the complex conjugate of $2 - 3i$?
2. How does multiplication by $i$ affect a complex number geometrically in the complex plane?

Complex Numbers (Mathematics > Algebra)

Definition

A complex number $z$ is a number of the form $a + bi$ , where $a$ and $b$ are real numbers and $i$ is the imaginary unit defined by $i^2 = -1$ . Formally:

\large z = a + bi, \quad \text{where } a, b \in \mathbb{R} \text{ and } i^2 = -1

Key Concepts

Real and imaginary parts
Complex plane representation
Modulus and argument
Complex conjugate

Important Properties

Closure: The sum and product of two complex numbers is a complex number
Commutativity: $z_1 + z_2 = z_2 + z_1$ and $z_1 \cdot z_2 = z_2 \cdot z_1$
Every complex number has a unique complex conjugate

Essential Formulas

Modulus: $|z| = \sqrt{a^2 + b^2}$
Euler’s formula: $e^{i\theta} = \cos\theta + i\sin\theta$

Core Examples

Simplify $(3 + 2i) + (1 - 5i)$
Find the roots of $z^2 + 1 = 0$

Fundamental Theorem of Algebra: Every non-constant polynomial equation has at least one complex root

Common Pitfalls

Forgetting that $i^2 = -1$ when simplifying expressions
Incorrectly applying properties of real numbers to complex numbers

[[Polar Form of Complex Numbers]]
[[Complex Roots of Unity]]

Quick Review Questions

What is the complex conjugate of $2 - 3i$ ?
How does multiplication by $i$ affect a complex number geometrically in the complex plane?

Why This Method Works For Me

This approach is effective for several reasons:

Preparation: The initial AI notes provide context, making the main lesson easier to follow. It’s like getting a movie trailer for the math lesson.
Active Learning: When I update my notes after the lesson, I’m not just passively absorbing – I’m actively engaging with the material. It’s like teaching it to myself.
Problem-Solving Skills: Working through problems independently deepens my understanding, even after commiting a mistake.
Consistent Practice: The repetitive nature of the process aids long-term retention, and the learning process doesn’t get monotonous.

Closing Thoughts

This method has transformed my approach to learning math. It combines the structured lessons from Math Academy with the flexibility of AI-generated notes, creating a personalized learning experience that keeps me engaged and helps me retain information better.

But remember, this is just what works for me. Learning is a personal journey, and what’s effective can vary from person to person. Maybe you have a completely different approach that works wonders for you, or perhaps you’re still searching for your ideal study method.

I’m curious to hear about your experiences. How do you tackle challenging math concepts? Have you experimented with any tech tools in your studies? Share your thoughts and strategies – who knows, we might all learn some new tricks to add to our mathematical toolboxes!

Keep exploring, keep learning, and most importantly, don’t be afraid to find your own path in the world of mathematics. After all, that’s what makes this journey so exciting ⭐