Navigating complex Math Academy lessons can be challenging. Over time, I’ve developed a structured approach that has significantly improved my understanding and retention of mathematical concepts. Let me walk you through my process, and hopefully it’ll speed up your learning journey.

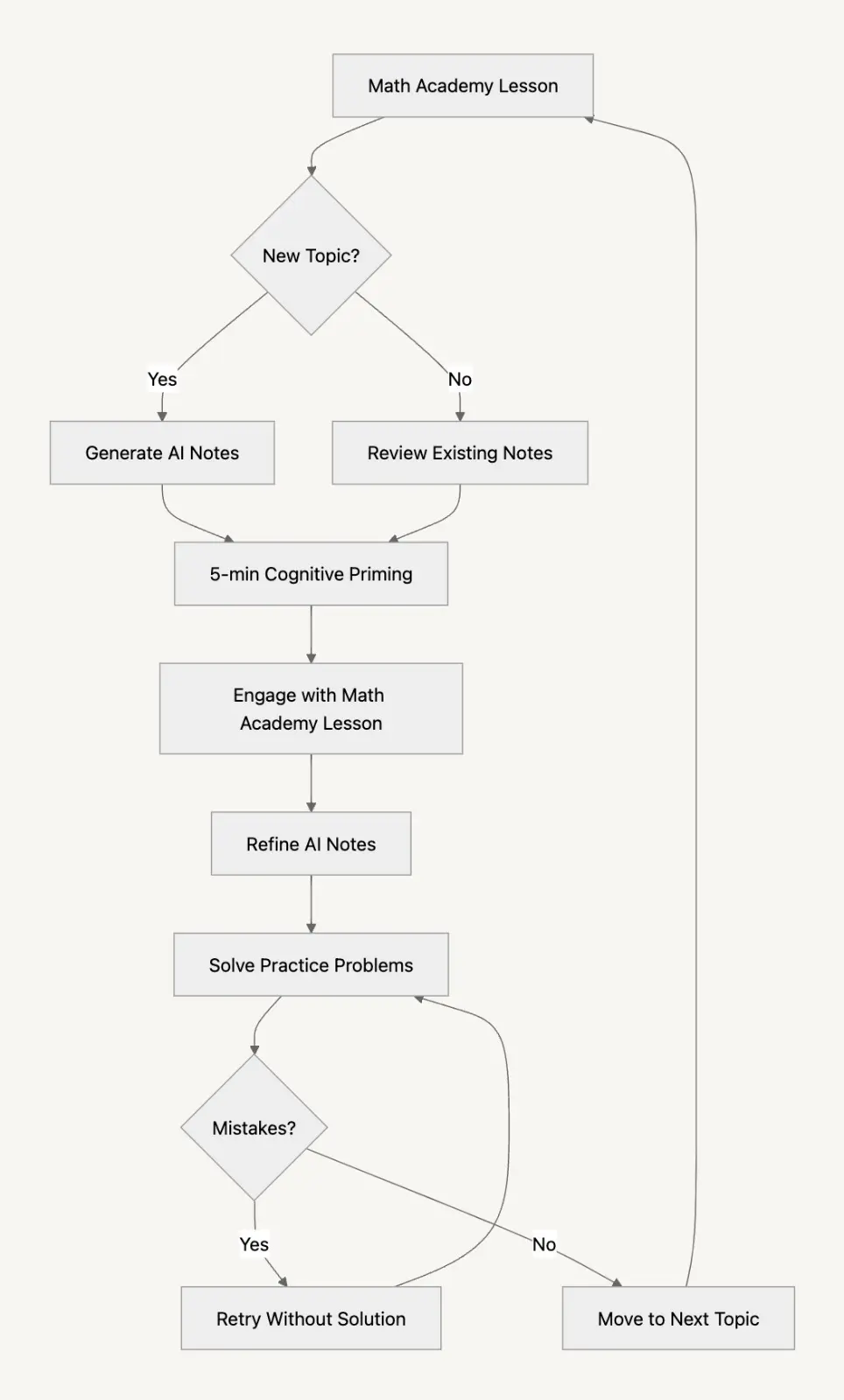
My Structured Approach

Here’s how I approach each new Math Academy lesson:

1. Topic Check: I start by asking, “Is this a new topic?”

   • For new topics, I use an AI tool to generate initial notes.
   • For familiar topics, I review my existing notes.

2. Quick Prep: I spend about 5 minutes reviewing the notes. This brief overview helps prime my brain for the lesson.

3. Math Academy Lesson: With this preparation, I find it easier to follow and engage with the actual lesson.

4. Note Refinement: After the lesson, I revisit my notes. I add new information, clarify points, and sometimes correct misunderstandings.

5. Practice Problems: Next, I tackle practice problems. When I make mistakes, I try to figure them out on my own before checking the solutions.

6. Repeat: I move on to the next topic and start the process again.

Create concise, clear mathematical notes in a fenced markdown code block on "[INSERT TOPIC]". Use the structure below:

# [Topic Name] ([Area] > [Subarea])
*(Example: "Mean (Mathematics > Statistics)" or "Complex Numbers (Mathematics > Algebra)")*

## Definition
- Provide a precise verbal explanation.
- Present the formal definition in LaTeX (e.g., for a dataset \(\{x_1, x_2, \dots, x_n\}\), the mean \(\bar{x}\) is given by: 
$$\bar{x} = \frac{1}{n}\sum_{i=1}^n x_i$$).

## Key Concepts
- List 3-4 fundamental ideas or principles.

## Important Properties
1. [State a key property or characteristic]
2. [State another property]
3. [Optional: Additional property]

## Essential Formulas
- Include the primary formula(s) in LaTeX.

## Core Examples
1. Provide a basic example that demonstrates the concept.
2. Offer a more advanced application or example.

## Related Theorems/Rules
- (If applicable) Mention important theorems or rules associated with the topic.

## Common Pitfalls
- Note a typical mistake or misconception.
- Optionally, list another common error.

## Related Topics
- List 1-2 closely related mathematical topics.

## Quick Review Questions & Answers
1. **Question:** [Pose a question that tests understanding of a key concept]
 **Answer:** [Provide a concise answer to the question]
2. **Question:** [Pose another question to encourage deeper analysis]
 **Answer:** [Provide a concise answer to the question]

# Complex Numbers (Mathematics > Algebra)

## Definition
A complex number $z$ is a number of the form $a + bi$, where $a$ and $b$ are real numbers and $i$ is the imaginary unit defined by $i^2 = -1$. Formally:

$$\large z = a + bi, \quad \text{where } a, b \in \mathbb{R} \text{ and } i^2 = -1$$

## Key Concepts
- Real and imaginary parts
- Complex plane representation
- Modulus and argument
- Complex conjugate

## Important Properties
1. Closure: The sum and product of two complex numbers is a complex number
2. Commutativity: $z_1 + z_2 = z_2 + z_1$ and $z_1 \cdot z_2 = z_2 \cdot z_1$
3. Every complex number has a unique complex conjugate

## Essential Formulas
- Modulus: $|z| = \sqrt{a^2 + b^2}$
- Euler's formula: $e^{i\theta} = \cos\theta + i\sin\theta$

## Core Examples
1. Simplify $(3 + 2i) + (1 - 5i)$
2. Find the roots of $z^2 + 1 = 0$

## Related Theorems/Rules
Fundamental Theorem of Algebra: Every non-constant polynomial equation has at least one complex root

## Common Pitfalls
- Forgetting that $i^2 = -1$ when simplifying expressions
- Incorrectly applying properties of real numbers to complex numbers

## Related Topics
- Polar Form of Complex Numbers
- Complex Roots of Unity

## Quick Review Questions
1. What is the complex conjugate of $2 - 3i$?
2. How does multiplication by $i$ affect a complex number geometrically in the complex plane?

Why This Method Works For Me

This approach is effective for several reasons:

1. Preparation: The initial AI notes provide context, making the main lesson easier to follow. It’s like getting a movie trailer for the math lesson.

2. Active Learning: When I update my notes after the lesson, I’m not just passively absorbing – I’m actively engaging with the material. It’s like teaching it to myself.

3. Problem-Solving Skills: Working through problems independently deepens my understanding, even after committing a mistake.

4. Consistent Practice: The repetitive nature of the process aids long-term retention, and the learning process doesn’t get monotonous.

Closing Thoughts

This method has transformed my approach to learning math. It combines the structured lessons from Math Academy with the flexibility of AI-generated notes, creating a personalized learning experience that keeps me engaged and helps me retain information better.

But remember, this is just what works for me. Learning is a personal journey, and what’s effective can vary from person to person. Maybe you have a completely different approach that works wonders for you, or perhaps you’re still searching for your ideal study method.

I’m curious to hear about your experiences. How do you tackle challenging math concepts? Have you experimented with any tech tools in your studies? Share your thoughts and strategies – who knows, we might all learn some new tricks to add to our mathematical toolboxes!

Keep exploring, keep learning, and most importantly, don’t be afraid to find your own path in the world of mathematics. After all, that’s what makes this journey so exciting ⭐